MissyElliott.encode("Example") # => "\xAE\xF0\xBC\xA4\xF8\xE4\xAC"

#"Example"
#--> ["E", "x", "a", "m", "p", "l", "e"]
#--> [69, 120, 97, 109, 112, 108, 101]
#--> ["01000101", "01111000", "01100001", "01101101", "01110000", "01101100", "01100101"]
# Shift yo bits down
#--> ["10001010", "11110000", "11000010", "11011010", "11100000", "11011000", "11001010"]
# Flip it
#--> ["01110101", "00001111", "00111101", "00100101", "00011111", "00100111", "00110101"]
# And reverse it
#--> ["10101110", "11110000", "10111100", "10100100", "11111000", "11100100", "10101100"]
#--> [174, 240, 188, 164, 248, 228, 172]
#--> ["\xAE", "\xF0", "\xBC", "\xA4", "\xF8", "\xE4", "\xAC"]
#--> "\xAE\xF0\xBC\xA4\xF8\xE4\xAC"

This is an excerpt from the README of a silly ruby gem I published, aptly named: missy_elliott. It is obvious, at a glance, that this encoding algorithm is easily reversible: You simply repeat the same 3 steps (“shift, flip, reverse”) in reverse order (“reverse, flip, un-shift”).

However, after further investigation, I noticed something strange: MissyElliott.encode, and MissyElliott.decode - despite having different implementations - are actually doing exactly the same thing!!

MissyElliott.encode("How is this even possible?!")
# => "\xF6\x84\x88\xFD\xB4\x98\xFD\xE8\xF4\xB4\x98\xFD\xAC\xC8\xAC\xC4\xFD\xF8\x84\x98\x98\xB4\xDC\xE4\xAC\x81\xBD"

MissyElliott.encode("\xF6\x84\x88\xFD\xB4\x98\xFD\xE8\xF4\xB4\x98\xFD\xAC\xC8\xAC\xC4\xFD\xF8\x84\x98\x98\xB4\xDC\xE4\xAC\x81\xBD")
# => "How is this even possible?!"

MissyElliott.decode("How is this even possible?!")
# => "\xF6\x84\x88\xFD\xB4\x98\xFD\xE8\xF4\xB4\x98\xFD\xAC\xC8\xAC\xC4\xFD\xF8\x84\x98\x98\xB4\xDC\xE4\xAC\x81\xBD"

MissyElliott.decode("\xF6\x84\x88\xFD\xB4\x98\xFD\xE8\xF4\xB4\x98\xFD\xAC\xC8\xAC\xC4\xFD\xF8\x84\x98\x98\xB4\xDC\xE4\xAC\x81\xBD")
# => "How is this even possible?!"

This completely threw me off when I first saw it - I figured there must be a bug in my code. But it’s true!

If you’d like to have a go at proving this for yourself, stop reading now. I’ll show my answer after the following message from my sponsor:

Reciprocal Ciphers

A reciprocal cipher is an encoding algorithm that is the inverse of itself. Perhaps the simplest, best-known example of such a cipher is ROT-13; a special case of the Caesar cipher.

The reason why ROT-13 is reciprocal is quite obvious: We shift each letter of the input down (or up!) 13 places in the alphabet. And, since there are 26 letters in the alphabet, repeating the process gets us back to where we started. For example:

"flip me" --> "syvc zr" --> "flip me"

But how on Earth does Missy Elliott manage this, with her much more complicated encoding?! Here’s one example, to show the reciprocal encoding in action:

ORIGINAL: 10011101

shift: 00111011

flip: 11000100

reverse: 00100011 (encoded)

shift: 01000110

flip: 10111001

reverse: 10011101 (twice encoded == ORIGINAL!!)

Is this always true? Can we prove it? Yes - here’s what I came up with:

We only need to consider what happens to an individual bit, when applying the Missy Elliot algorithm (twice). Each bit an be precisely described by two things: its value (1 or 0), and its position (how many bits are to the left/right).

Without loss of generality, let’s consider what happens to a single bit, of value B (the opposite of which is b), which has x bits to its left (and for the sake of clarity, y bits to its right). The following syntax should be fairly self explanatory:

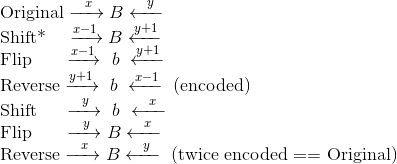
*There is a slight edge case here, which I have omitted: What happens when x=0, i.e. the bit is “shifted” onto the back of the list? However, this is a fairly trivial edge case to cover; I leave this as an exercise for the reader. (I’ve always wanted to use that phrase, after having it drilled into me at university!)

Missy Elliott’s Graph

Missy Elliott’s algorithm essentially works by mapping each character’s ASCII code to an “encoded” number, then converting it back to the corresponding character in the ASCII table. Since the algorithm is reciprocal, this creates a 1-to-1 pairing between ASCII codes when repeating the encoding.

For example:

0 = 00000000 <--> 11111111 = 255
1 = 00000001 <--> 10111111 = 191
2 = 00000010 <--> 11011111 = 223

Do you wonder what it would look like to plot all 256 points on a scatter graph? Well, I did:

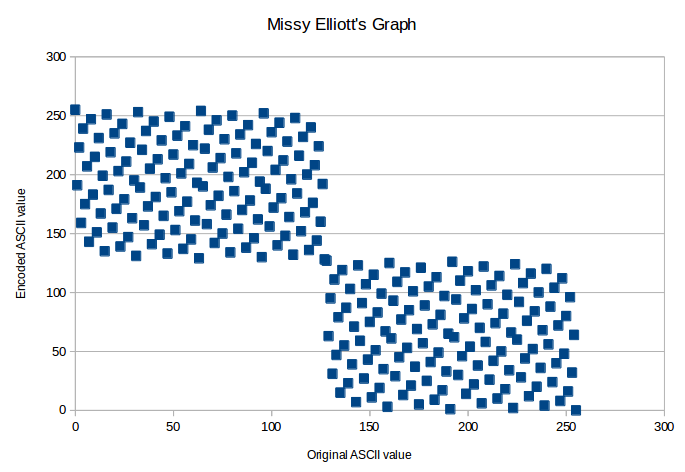
The obvious property that this graph shows is: If x<128, then Encoding(x) >=128 (and vice versa). Proving this is quite easy:

Using similar technique to the above proof, only in this case B represents 7 digits, rather than just 1 (and b represents its “flipped” value), consider what happens when we apply the Missy Elliott encoding to any number < 128:

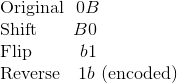
In other words, if the original value starts with a 0 (i.e. is < 128) then its encoded value must start with a 1 (i.e. is >= 128). However, there is a far more interesting (less obvious) feature of this graph: it always oscillates in value…

Encoding(0) = 255 > Encoding(1) = 191 < Encoding(2) = 223 > Encoding(3) = 159 < ...

… Except for one point, in the middle:

Encoding(126) = 192 > Encoding(127) = 128 > Encoding(128) = 127 > Encoding(129) = 64
                                         ^^^

This can be visualised by taking a subsection of the above graph:

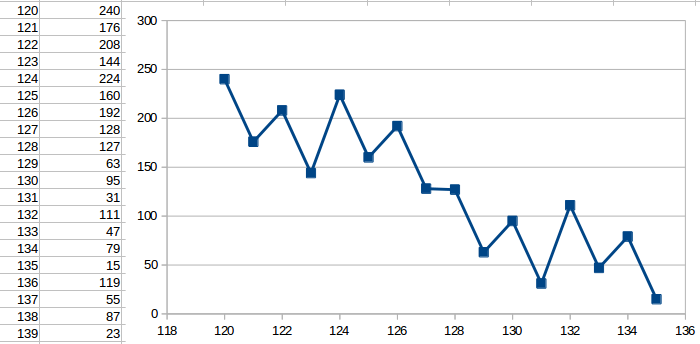
In fact, this sequence has an even crazier property hiding beneath the surface. Let’s only look at the second half of the mappings, i.e.

Encoding(128), Encoding(129), ..., Encoding(255)

This sub-sequence is equal to:

127, 63, 95, 31, 111, 47, 79, 15, 119, 55, 87, 23, 103, 39, 71, 7, 123, 59, 91, 27, 107, 43, 75, 11, 115, 51, 83, 19, 99, 35, 67, 3, 125, 61, 93, 29, 109, 45, 77, 13, 117, 53, 85, 21, 101, 37, 69, 5, 121, 57, 89, 25, 105, 41, 73, 9, 113, 49, 81, 17, 97, 33, 65, 1, 126, 62, 94, 30, 110, 46, 78, 14, 118, 54, 86, 22, 102, 38, 70, 6, 122, 58, 90, 26, 106, 42, 74, 10, 114, 50, 82, 18, 98, 34, 66, 2, 124, 60, 92, 28, 108, 44, 76, 12, 116, 52, 84, 20, 100, 36, 68, 4, 120, 56, 88, 24, 104, 40, 72, 8, 112, 48, 80, 16, 96, 32, 64, 0

Perfect Oscillating Sequences

Disclaimer: I have no idea if sequences with this property have ever been named before; I certainly cannot find one! I invented the name “perfect oscillating”, but if you feel an alternative name is more suiting, or are aware of pre-existing name, please let me know in the comments!

Let’s take a look at a few sub-sequences of the above:

(a_2n) = 63, 31, 47, 15, 55, 23, 39, 7, 59, 27, ...
(a_3n) = 95, 47, 119, 23, 71, 59, 107, 11, 83, ...
(a_4n) = 31, 15, 23, 7, 27, 11, 19, 3, 29, 13, ...
(a_2n-1) = 127, 95, 111, 79, 119, 87, 103, 71, 123, ...
(a_5n-3) = 63, 79, 23, 123, 43, 83, 3, 109, 53, 69, ...

Any sub-sequence of the form (a_xn+y) also oscillates!!

As it turns out, Missy Elliott’s song is all about a novel way to generate the sequence: A030109[7]. Who would have guessed?!

In fact, there’s one very useful application for sequences like these - the answer might come as a surprise!

To keep things simple from here on, let’s use a somewhat shorter sequence. The following perfect oscillating sequence can also be generated using the Missy Elliott algorithm (on the numbers 0 - 7), and adding 1 to each term:

8, 4, 6, 2, 7, 3, 5, 1

I found a clue for how this sequence is used, in the comments for A049773. To summarise, this is the “optimally fair” starting line-up for ranked players in a knock-out tournament! Assuming the favourite always wins, the result of such a tournament would look like this:

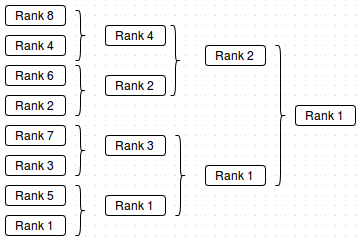
Missy Elliott truly is a lyrical genius, after all.

Phew, well that got a little side-tracked from the original purpose of this blog post!

Was it worth it?